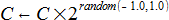A few years ago I implemented a card game I knew from my high school years into a mobile app. I had written an AI for it, but I wasn’t satisfied with its skill level. Not convinced it was worth to further manually code a better solution, I looked into AI algorithms and ended up at Genetic Programming (GP). To make a long story short, it worked so well that the AI plays better than I do. GP is easy to conceptually understand and reasonably simple to implement at a basic level, which is what this article is about. Be warned, this article does not teach you how to program in general.
This article has two sections: One section to introduce GP, and one section to describe the example project.
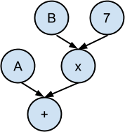
GP starts with ‘genetic’ because it is inspired from a process in nature called evolution. It is a subclass of Genetic Algorithms (GA) that deals with “programs” represented by tree graphs. By running a genetic program, you can perform a computation, make a decision, or generally execute some sequence of events. An example is shown below of a genetic program that calculates A + B * 7.
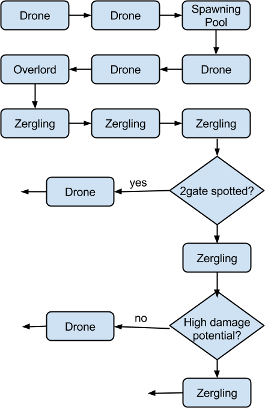
Here’s another genetic program that executes an 8 pool Starcraft 2 build order intro (disclaimer: this is my interpretation based on a description on a popular SC2 site). Note that this is still a tree structure, although it’s drawn in a non-standard manner. How to evaluate this tree should be straightforward except for the decision nodes, whose conditions might be difficult to implement; “high damage potential” is a fuzzy concept.
The ‘genetic’ part comes from the fact that these trees/programs can be considered genomes that can be “mutated” (changed) in various ways. By having a population of different genomes/programs mutating through successive generations, while applying fitness/selection criteria, we can influence what tasks the genetic programs become good at solving. Let those individual programs that best solve the task have the largest genetic influence on the next generation - this is evolution!
The image below shows an (unrealistically tiny) population of four individuals undergoing evolution for five generations through random color change and node addition/removal, where the task is to have as many blue nodes as possible. Of course, this is a contrived example given that we know how to make a huge blue tree.
Note how the best trees are either cloned or subjected to mutation, which may or may not result in a more fit child. Cloning ensures good trees survive in unaltered form, but slow down mutation (in huge populations cloning isn’t really necessary). Also note how selection rules are not necessarily 100% fair; it doesn’t matter.
Finally, let me clarify on what makes GP different from genetic algorithms. GA in general is about optimization of parameters through evolution, a form of stochastic search. How those parameters are combined is nothing GA concerns itself with, except in specific cases such as GP. GP on the other hand provides a way of not only evolving parameter values, but also how those parameters are combined, making it a more powerful learning approach. Even if you don’t know the expression for a certain computation, GP can learn it for you rather than just optimize a set of input parameters!
Arithmetic tree
The easiest and I suspect most common use of GP is to let programs represent arithmetic expressions, most commonly expressions on “real” numbers (OK, computer floating precision aside). We have already looked at this earlier, but suffice to say that the ability to evolve a mathematical function for some purpose is a powerful one. Below shows an evaluation function in Lua evolved for a “medium” level AI in my game:
Note how there are terminals (leaves) such as env.rounds, math.random() and constants, and the binary nonterminals + and *. Note that nonterminals in arithmetic trees don’t in general need any extra parameters - just receive them as input branches. The whole thing is very confusing when read with parentheses in a linear text file, so let’s draw the tree:
This tree form is what’s actually stored in memory while evolution and simulation are running; the linear code is only an export optimized for my target game. Another interesting thing to note is the constant result computation -4.0745883 + 0.025403308, such redundancy and overgrowth (huge sub-trees of dubious utility) may be controlled with the fitness function as we shall see later.
Execution tree
Another option is to let a genetic program represent a computer program in a more traditional sense, i.e. a control flow graph. Of course, a major restriction compared to a normal computer program is the fact that the graph must be a tree. This may or may not be a problem, and there are ways to work around the lack of loops through innovative node types.
The Starcraft 2 build order example earlier is an example of an execution tree; execution in that case occurs from root to leaves with decisions in-between. Nodes may either be decisions (needing annotated parameters) or simply execute an instruction with a linear result, such as “build worker”. Some instruction nodes may have no children at all and thus effectively can function as leaves as well.
A less generally useful but mentionable option is you might actually reverse definition of flow direction and execute from a certain start leaf to the root in a predictable linear path. In that case, execution might be seen as going from a specific to a more generalized conclusion, in which different specific start conditions share a consequence.
Decision tree
Decision trees are tree graphs that are evaluated from root to leaves, following a path of decisions from the root that eventually end up with a leaf consequence/classification. This is without any non-standard execution in the nonterminals - all nonterminals are pure decisions. Note that decision trees have been studied extensively and that there are likely better algorithms than GP if you need to build a decision tree. Yet, it’s worth mentioning the possibility.
Note that in decision tree flow graph notation, nonterminals are indicated with multiple graphical elements:
Like for execution trees, nonterminals in decision trees are more complex than for arithmetic trees since extra parameters such as conditions or probabilities need to be annotated. Possibly, these parameters also need to be mutated directly for more efficient learning, rather than just being initialized randomly at node creation.
Although only cloning and mutation were mentioned so far, there are in fact several fundamental genetic operations that can be applied on a GP tree.
Cloning
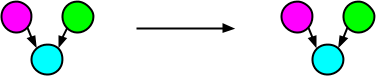
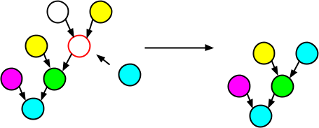
The easiest operation to understand is cloning, in which an identical copy of the parent/source tree is returned. I will avoid the term “parent” because it conflicts with tree graph terminology, and instead call parents source trees further on in this text. Similarly, I will avoid the term child (even though these terms are present in the source code). Anyway, here is an example of a cloning operation on a source tree:
Mutation
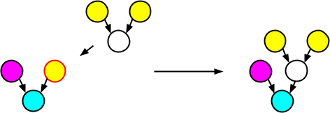
Mutation involves making some sort of change to a single source tree. In a GP tree, it is possible to replace a subtree on a branch of the source tree with a random tree. This will in fact cover most cases of tree alteration you can think of: It can both grow the tree or shrink the tree, depending on the maximum depth of the random tree generated.
A good max depth for the random subtree seems to be 2 (allowing at most one nonterminal). If it were 1, trees would never grow through mutation, and much larger and your trees will rapidly grow to be filled with loads of random crap, excuse the expression.
For cases where parameters on nonterminals are required, you might want to include code to mutate these parameters without replacing trees. Similarly, if you have constant terminals in an arithmetic tree, you might want to controllably mutate these. Consider that a better solution often lies close to an already good solution, and completely throwing a constant out of the window to replace it with a completely random value as occurs with subtree replacement is not likely to be particularly successful.
Above is the constant update rule I use. Note that the magnitude is exponentially altered, from 0.5 to 2. The sign is intentionally never changed. In expressions such as A * B, it turns out that changing the sign of one of the operands has a rather dramatic effect - it changes the sign of the result as well. For changing signs, I instead rely on the node replacement covered earlier.
Crossover
Did you ever wonder why you have two biological parents and not one? Now you will know!
The limitation of mutation is that random data isn’t likely to do anything useful. Meanwhile, your population hopefully already contains a diversity of useful genetic programs. A key insight here is that the subtrees of a genetic tree may be useful sub-solutions to the task. Thus, rather than replacing a branch with random data, we replace it with a subtree of a proven useful source tree.
Crossover, as this is known, means you combine the traits of two source trees. The results will not always be successful, but overall the chances of something interesting resulting are comparatively good. Crossover will speed up evolution since different successful sub-solutions will be shared among different lineages without having to develop independently through mutation.
I didn't include an image because crossover looks similar to mutation, except the donor tree isn't random, but a randomly selected subtree of an individual.
Throughout this article we have assumed that there is a driving force behind evolution, guiding the evolution of genetic programs towards solving a particular task. That force is the fitness for the task.
How you define fitness is domain specific, but for GP a good start is as a function that can be used to order the population. The fitness function of an individual should be based on how efficient it is at the task (whether it is to win, to survive, etc). For instance, in a game with win/lose outcomes you might base fitness on N_wins / (N_wins + N_losses).
There is another important aspect of the fitness function; it can be used to protect against overgrowth. Overgrowth was briefly mentioned earlier, and it is a huge danger to the efficiency of evolution in some GP setups. Consider how efficient the expression 0 * (abs(sin(x)) ^ 5.88 + 72.21 - 28.01 * min(-827.17, x)) really is. In practice, rather than exactly 0, you might see constants evolving to some very small values when evolution tries to get rid of useless subtrees. The full effect of this can be unlimited growth of useless subtrees throughout the population, slowing down evolution to snail’s pace, or worse.
The problem, of course, is that there’s no penalty for useless arithmetic in the AI code included in the game simulation. But rather than trying to add that to the simulation (which would break the game rules), we can add the penalty to the fitness function. A good start (if rough) is basing the penalty on the size of the GP tree. For instance, here’s the fitness function I use in Sevens:
Overgrowth might be less of a problem with execution trees than arithmetic trees since fitness will be influenced directly by the simulation cost of executing instructions; building a worker does not take zero resources in reference to Starcraft 2. On the other hand, decision nodes might consistently leave a branch unvisited in which case the subtree on that branch will be dead weight memory-wise.
There’s another important detail yet to discuss, and it is how we select what genetic operations to apply to the individuals in each generation. First, here’s how my rather crude implementation works (approximately) for each generation:
The split_O values should add up to 1 to keep the population at the same size between generations. These values let you assign how large of a percentage of each population should be submitted to each type of genetic operation. In practice, I use 10% cloning, 45% constant mutation, 22.5% tree mutation and 22.5% crossover. You’ll have to experiment with what works for you.
GP is great since it (for example) can really learn entire functions independently, right? Yes, but only under certain conditions. To use arithmetic trees for AI agent evaluation functions as an example: First, you need to specify what the outputs of your functions mean, and in what context they will apply. Secondly, you need to describe the state of the environment with terminal nodes accurately for agents to be able to make informed decisions. Thirdly, you need to think about the set of nonterminal nodes. Including all possible binary functions on real numbers in mathematics you can think of is not necessarily useful and evolution will likely be much faster and stable with a limited set of nonterminal operators.
Genetic programs share the same weakness with GA in general; a large number of generations with a large number of individuals must be computed for any learning/optimization to happen. This pretty much means GP is too slow for any online adjustment to the genomes. You need to be able to do batch-processing to execute a huge number of trials in advance (offline), and that entails having a simulation of the world. Consequently, GP is more suitable for games (on the condition they have batch processable simulation cores) than e.g. robotics, for which it is harder to produce simulations of the environment the agents operate in.
GP and GA are random searches that will be outclassed by search algorithms that are better suited to the problem space, and should be seen as a last resort or “I don’t care if it takes longer”-option. There are no silver bullets in AI; always investigate a lot before picking your approach or you end up wasting your time.
The code attached with this article is the command line simulation and evolution tool in Java/Eclipse I developed in tandem with my app. The Lua source of my original app is not something anyone would like to view anyhow.
In the game of Sevens, the decisions that need to be made by an agent are of a very basic nature: Select the best card in two different contexts, when playing or “sending” a card to a player lacking a playable card. So, we can calculate a (utility) value for a certain action (a playable card), and we can pick the action with the best value. This is a reasonable way of modelling the decision structure of the game, and its simplicity means we can evolve basic arithmetic functions with GP for calculating the values from the state of the game for a particular action and context.
Sevens is a highly stochastic game in which the outcome is often decided by the cards dealt, so the fact that a player happens to win a single round does not imply superiority. However, the law of large numbers applies and if you play 1000 games of which agent A pitted against B and C wins 500 you can reasonably assume A is the better agent. A word of warning though: Some games display non-transitive relations when comparing skill levels of various agents, and although I couldn’t find this to be the case in Sevens, it may make it necessary to be very careful in how you select agents to be pitted against one-another to ensure they meet varied opposition.
The tool simply executes from SevenGP.main() without taking any parameters or input. Thus, it’s preferable to work from within Eclipse so you can modify the main function as needed. If you feel an urge to rant about this, consider that you will not be executing this kind of tool with changed input parameters very many times. You can download Eclipse for free here.
The tool generates a file called computer.txt in the project directory, containing the Lua exported evaluation functions. I’ve left a default generated file there for your interest. Notice how at both easy and medium, many of the functions are downright trivial consisting of a single terminal - this is due to the stochastic nature of the game and the fact 0 versus 1 generations were executed for these skill levels. Only at hard with 11 generations you start seeing more interesting evaluation functions. I commented out the expert level as it’s not necessary for demo purposes and it takes a while with 111 generations.
I would recommend you rewrite the code in your favorite language and for your own game (while making improvements), in order to understand it. Try to avoid language mismatches like the Java/Lua mismatch in this implementation, since it is certainly preferable to be able to share game simulation code rather than rewriting it in two languages. Nothing prevents you from generating e.g. C# code from C# (heck, in .NET even at runtime if desirable) if you’re concerned about the efficiency of the intermediate tree representation.
You might find it possible to directly reuse this code in JVM projects - feel free to do so, although refactoring is still recommended. I did not intend this to be used as a library and I have no desire to start reworking it into one myself.
Speaking of libraries, there probably are a couple to be found on the Internet in case you want to use a ready-made solution rather than do-it-yourself. If you feel confident you understand GP sufficiently or need a solution for a production level game, it’s likely the better option.
.sevengp package: Contains the main class SevenGP which you’ll probably want to get reading/playing around with right away.
.sevengp.game package: Contains the game simulation. Read up on this if you want to understand the game rules clearly, but you don’t really need to.
.gp package: Some base classes and interfaces for GP development, not particularly likely to be of generic use nonetheless. The Individual class is quite interesting, since it contains implementations of the genetic operations in its constructors.
.sevengp.gp package: Extensions to the base GP package and player class for Sevens.
.sevengp.gp.alphabet package: Terminals and nonterminals for Sevens. Many operations reside here in object oriented fashion (aspect oriented programming might have been more appropriate). Reading these are quite recommended.
There’s some confusion in the code regarding the term “individual”. The Individual class only represents a single tree, whereas the Specimen class is a true individual, specifically tailored for the game of Sevens with two different trees for play and send contexts. There are more terms that might be confused, as a disclaimer.
Hopefully this helps beginners to understand GP a bit better, and possibly giving them that final nudge that causes all pieces of the puzzle to fall in the right places and give sufficient understanding to implement GP. In my (subjective) opinion, GP isn’t a difficult concept at all, and can be a very useful tool in the gameplay programmer’s arsenal. Just make sure it’s the best option before you spend time applying it to a problem.
Top image credit: GECCO
This article has two sections: One section to introduce GP, and one section to describe the example project.
Introduction to GP
GP starts with ‘genetic’ because it is inspired from a process in nature called evolution. It is a subclass of Genetic Algorithms (GA) that deals with “programs” represented by tree graphs. By running a genetic program, you can perform a computation, make a decision, or generally execute some sequence of events. An example is shown below of a genetic program that calculates A + B * 7.
Here’s another genetic program that executes an 8 pool Starcraft 2 build order intro (disclaimer: this is my interpretation based on a description on a popular SC2 site). Note that this is still a tree structure, although it’s drawn in a non-standard manner. How to evaluate this tree should be straightforward except for the decision nodes, whose conditions might be difficult to implement; “high damage potential” is a fuzzy concept.
The ‘genetic’ part comes from the fact that these trees/programs can be considered genomes that can be “mutated” (changed) in various ways. By having a population of different genomes/programs mutating through successive generations, while applying fitness/selection criteria, we can influence what tasks the genetic programs become good at solving. Let those individual programs that best solve the task have the largest genetic influence on the next generation - this is evolution!
The image below shows an (unrealistically tiny) population of four individuals undergoing evolution for five generations through random color change and node addition/removal, where the task is to have as many blue nodes as possible. Of course, this is a contrived example given that we know how to make a huge blue tree.
Note how the best trees are either cloned or subjected to mutation, which may or may not result in a more fit child. Cloning ensures good trees survive in unaltered form, but slow down mutation (in huge populations cloning isn’t really necessary). Also note how selection rules are not necessarily 100% fair; it doesn’t matter.
Finally, let me clarify on what makes GP different from genetic algorithms. GA in general is about optimization of parameters through evolution, a form of stochastic search. How those parameters are combined is nothing GA concerns itself with, except in specific cases such as GP. GP on the other hand provides a way of not only evolving parameter values, but also how those parameters are combined, making it a more powerful learning approach. Even if you don’t know the expression for a certain computation, GP can learn it for you rather than just optimize a set of input parameters!
Some examples of what a GP tree can represent
Arithmetic tree
The easiest and I suspect most common use of GP is to let programs represent arithmetic expressions, most commonly expressions on “real” numbers (OK, computer floating precision aside). We have already looked at this earlier, but suffice to say that the ability to evolve a mathematical function for some purpose is a powerful one. Below shows an evaluation function in Lua evolved for a “medium” level AI in my game:
(((((env.rounds)+((env.suit)*(env.rank)))+(env.safe))+((env.block)*(env.block)))*(((-4.0745883)+(0.025403308))+((((env.selfblock)*(env.dist))+((env.selfblock)*(env.safe)))+(math.random()))))
Note how there are terminals (leaves) such as env.rounds, math.random() and constants, and the binary nonterminals + and *. Note that nonterminals in arithmetic trees don’t in general need any extra parameters - just receive them as input branches. The whole thing is very confusing when read with parentheses in a linear text file, so let’s draw the tree:
This tree form is what’s actually stored in memory while evolution and simulation are running; the linear code is only an export optimized for my target game. Another interesting thing to note is the constant result computation -4.0745883 + 0.025403308, such redundancy and overgrowth (huge sub-trees of dubious utility) may be controlled with the fitness function as we shall see later.
Execution tree
Another option is to let a genetic program represent a computer program in a more traditional sense, i.e. a control flow graph. Of course, a major restriction compared to a normal computer program is the fact that the graph must be a tree. This may or may not be a problem, and there are ways to work around the lack of loops through innovative node types.
The Starcraft 2 build order example earlier is an example of an execution tree; execution in that case occurs from root to leaves with decisions in-between. Nodes may either be decisions (needing annotated parameters) or simply execute an instruction with a linear result, such as “build worker”. Some instruction nodes may have no children at all and thus effectively can function as leaves as well.
A less generally useful but mentionable option is you might actually reverse definition of flow direction and execute from a certain start leaf to the root in a predictable linear path. In that case, execution might be seen as going from a specific to a more generalized conclusion, in which different specific start conditions share a consequence.
Decision tree
Decision trees are tree graphs that are evaluated from root to leaves, following a path of decisions from the root that eventually end up with a leaf consequence/classification. This is without any non-standard execution in the nonterminals - all nonterminals are pure decisions. Note that decision trees have been studied extensively and that there are likely better algorithms than GP if you need to build a decision tree. Yet, it’s worth mentioning the possibility.
Note that in decision tree flow graph notation, nonterminals are indicated with multiple graphical elements:
Like for execution trees, nonterminals in decision trees are more complex than for arithmetic trees since extra parameters such as conditions or probabilities need to be annotated. Possibly, these parameters also need to be mutated directly for more efficient learning, rather than just being initialized randomly at node creation.
Genetic operations
Although only cloning and mutation were mentioned so far, there are in fact several fundamental genetic operations that can be applied on a GP tree.
Cloning
The easiest operation to understand is cloning, in which an identical copy of the parent/source tree is returned. I will avoid the term “parent” because it conflicts with tree graph terminology, and instead call parents source trees further on in this text. Similarly, I will avoid the term child (even though these terms are present in the source code). Anyway, here is an example of a cloning operation on a source tree:
Mutation
Mutation involves making some sort of change to a single source tree. In a GP tree, it is possible to replace a subtree on a branch of the source tree with a random tree. This will in fact cover most cases of tree alteration you can think of: It can both grow the tree or shrink the tree, depending on the maximum depth of the random tree generated.
A good max depth for the random subtree seems to be 2 (allowing at most one nonterminal). If it were 1, trees would never grow through mutation, and much larger and your trees will rapidly grow to be filled with loads of random crap, excuse the expression.
For cases where parameters on nonterminals are required, you might want to include code to mutate these parameters without replacing trees. Similarly, if you have constant terminals in an arithmetic tree, you might want to controllably mutate these. Consider that a better solution often lies close to an already good solution, and completely throwing a constant out of the window to replace it with a completely random value as occurs with subtree replacement is not likely to be particularly successful.
Above is the constant update rule I use. Note that the magnitude is exponentially altered, from 0.5 to 2. The sign is intentionally never changed. In expressions such as A * B, it turns out that changing the sign of one of the operands has a rather dramatic effect - it changes the sign of the result as well. For changing signs, I instead rely on the node replacement covered earlier.
Crossover
Did you ever wonder why you have two biological parents and not one? Now you will know!
The limitation of mutation is that random data isn’t likely to do anything useful. Meanwhile, your population hopefully already contains a diversity of useful genetic programs. A key insight here is that the subtrees of a genetic tree may be useful sub-solutions to the task. Thus, rather than replacing a branch with random data, we replace it with a subtree of a proven useful source tree.
Crossover, as this is known, means you combine the traits of two source trees. The results will not always be successful, but overall the chances of something interesting resulting are comparatively good. Crossover will speed up evolution since different successful sub-solutions will be shared among different lineages without having to develop independently through mutation.
I didn't include an image because crossover looks similar to mutation, except the donor tree isn't random, but a randomly selected subtree of an individual.
Fitness and limiting overgrowth
Throughout this article we have assumed that there is a driving force behind evolution, guiding the evolution of genetic programs towards solving a particular task. That force is the fitness for the task.
How you define fitness is domain specific, but for GP a good start is as a function that can be used to order the population. The fitness function of an individual should be based on how efficient it is at the task (whether it is to win, to survive, etc). For instance, in a game with win/lose outcomes you might base fitness on N_wins / (N_wins + N_losses).
There is another important aspect of the fitness function; it can be used to protect against overgrowth. Overgrowth was briefly mentioned earlier, and it is a huge danger to the efficiency of evolution in some GP setups. Consider how efficient the expression 0 * (abs(sin(x)) ^ 5.88 + 72.21 - 28.01 * min(-827.17, x)) really is. In practice, rather than exactly 0, you might see constants evolving to some very small values when evolution tries to get rid of useless subtrees. The full effect of this can be unlimited growth of useless subtrees throughout the population, slowing down evolution to snail’s pace, or worse.
The problem, of course, is that there’s no penalty for useless arithmetic in the AI code included in the game simulation. But rather than trying to add that to the simulation (which would break the game rules), we can add the penalty to the fitness function. A good start (if rough) is basing the penalty on the size of the GP tree. For instance, here’s the fitness function I use in Sevens:
float getFitness() {
int size = play.getTreeSize() + send.getTreeSize();
int factor = Math.max(0, size - 20);
return getWinRatio() - factor * 0.0004f;
}
Overgrowth might be less of a problem with execution trees than arithmetic trees since fitness will be influenced directly by the simulation cost of executing instructions; building a worker does not take zero resources in reference to Starcraft 2. On the other hand, decision nodes might consistently leave a branch unvisited in which case the subtree on that branch will be dead weight memory-wise.
Evolution
There’s another important detail yet to discuss, and it is how we select what genetic operations to apply to the individuals in each generation. First, here’s how my rather crude implementation works (approximately) for each generation:
New population := {}, population = (already initialized)
Run simulation on population
Sort population according to fitness in descending order
For each genetic operation O:
N := split_O * N_population
For i = 1, N:
Source := population[i]
Emit individual in new population using O(Source)
Population := new population
The split_O values should add up to 1 to keep the population at the same size between generations. These values let you assign how large of a percentage of each population should be submitted to each type of genetic operation. In practice, I use 10% cloning, 45% constant mutation, 22.5% tree mutation and 22.5% crossover. You’ll have to experiment with what works for you.
Why not do GP
GP is great since it (for example) can really learn entire functions independently, right? Yes, but only under certain conditions. To use arithmetic trees for AI agent evaluation functions as an example: First, you need to specify what the outputs of your functions mean, and in what context they will apply. Secondly, you need to describe the state of the environment with terminal nodes accurately for agents to be able to make informed decisions. Thirdly, you need to think about the set of nonterminal nodes. Including all possible binary functions on real numbers in mathematics you can think of is not necessarily useful and evolution will likely be much faster and stable with a limited set of nonterminal operators.
Genetic programs share the same weakness with GA in general; a large number of generations with a large number of individuals must be computed for any learning/optimization to happen. This pretty much means GP is too slow for any online adjustment to the genomes. You need to be able to do batch-processing to execute a huge number of trials in advance (offline), and that entails having a simulation of the world. Consequently, GP is more suitable for games (on the condition they have batch processable simulation cores) than e.g. robotics, for which it is harder to produce simulations of the environment the agents operate in.
GP and GA are random searches that will be outclassed by search algorithms that are better suited to the problem space, and should be seen as a last resort or “I don’t care if it takes longer”-option. There are no silver bullets in AI; always investigate a lot before picking your approach or you end up wasting your time.
Example project
The code attached with this article is the command line simulation and evolution tool in Java/Eclipse I developed in tandem with my app. The Lua source of my original app is not something anyone would like to view anyhow.
The game
In the game of Sevens, the decisions that need to be made by an agent are of a very basic nature: Select the best card in two different contexts, when playing or “sending” a card to a player lacking a playable card. So, we can calculate a (utility) value for a certain action (a playable card), and we can pick the action with the best value. This is a reasonable way of modelling the decision structure of the game, and its simplicity means we can evolve basic arithmetic functions with GP for calculating the values from the state of the game for a particular action and context.
Sevens is a highly stochastic game in which the outcome is often decided by the cards dealt, so the fact that a player happens to win a single round does not imply superiority. However, the law of large numbers applies and if you play 1000 games of which agent A pitted against B and C wins 500 you can reasonably assume A is the better agent. A word of warning though: Some games display non-transitive relations when comparing skill levels of various agents, and although I couldn’t find this to be the case in Sevens, it may make it necessary to be very careful in how you select agents to be pitted against one-another to ensure they meet varied opposition.
Running the tool
The tool simply executes from SevenGP.main() without taking any parameters or input. Thus, it’s preferable to work from within Eclipse so you can modify the main function as needed. If you feel an urge to rant about this, consider that you will not be executing this kind of tool with changed input parameters very many times. You can download Eclipse for free here.
The tool generates a file called computer.txt in the project directory, containing the Lua exported evaluation functions. I’ve left a default generated file there for your interest. Notice how at both easy and medium, many of the functions are downright trivial consisting of a single terminal - this is due to the stochastic nature of the game and the fact 0 versus 1 generations were executed for these skill levels. Only at hard with 11 generations you start seeing more interesting evaluation functions. I commented out the expert level as it’s not necessary for demo purposes and it takes a while with 111 generations.
How to adapt for own needs
I would recommend you rewrite the code in your favorite language and for your own game (while making improvements), in order to understand it. Try to avoid language mismatches like the Java/Lua mismatch in this implementation, since it is certainly preferable to be able to share game simulation code rather than rewriting it in two languages. Nothing prevents you from generating e.g. C# code from C# (heck, in .NET even at runtime if desirable) if you’re concerned about the efficiency of the intermediate tree representation.
You might find it possible to directly reuse this code in JVM projects - feel free to do so, although refactoring is still recommended. I did not intend this to be used as a library and I have no desire to start reworking it into one myself.
Speaking of libraries, there probably are a couple to be found on the Internet in case you want to use a ready-made solution rather than do-it-yourself. If you feel confident you understand GP sufficiently or need a solution for a production level game, it’s likely the better option.
Structure of code
.sevengp package: Contains the main class SevenGP which you’ll probably want to get reading/playing around with right away.
.sevengp.game package: Contains the game simulation. Read up on this if you want to understand the game rules clearly, but you don’t really need to.
.gp package: Some base classes and interfaces for GP development, not particularly likely to be of generic use nonetheless. The Individual class is quite interesting, since it contains implementations of the genetic operations in its constructors.
.sevengp.gp package: Extensions to the base GP package and player class for Sevens.
.sevengp.gp.alphabet package: Terminals and nonterminals for Sevens. Many operations reside here in object oriented fashion (aspect oriented programming might have been more appropriate). Reading these are quite recommended.
There’s some confusion in the code regarding the term “individual”. The Individual class only represents a single tree, whereas the Specimen class is a true individual, specifically tailored for the game of Sevens with two different trees for play and send contexts. There are more terms that might be confused, as a disclaimer.
Final words
Hopefully this helps beginners to understand GP a bit better, and possibly giving them that final nudge that causes all pieces of the puzzle to fall in the right places and give sufficient understanding to implement GP. In my (subjective) opinion, GP isn’t a difficult concept at all, and can be a very useful tool in the gameplay programmer’s arsenal. Just make sure it’s the best option before you spend time applying it to a problem.
Top image credit: GECCO