For a beginner, geometry in 3D space may seem a bit daunting. 2D on paper was hard enough, but now, geometry in 3D?
Good news: use of trigonometry in graphics is rare and avoided for multitude of reasons. We have other tools which are easier to understand and use. You may recognize our old friend here - a vector.
![Attached Image: file(2).png]()
This article will introduce you to 3D vectors and will walk you through several real-world usage examples. Even though it focuses on 3D, most things explained here also work for 2D.
Article assumes familiarity with algebra and geometry, some programming language, a basic knowledge of OOP.
In mathematics, a vector is a construct that represents both a direction as well as a magnitude. In game development it often can be used to describe a change in position, and can be added or subtracted to other vectors. You would usually find a vector object as part of some math or physics library.
They typically contain one or more components such as x, y and z. Vectors can be 1D (contain only x), 2D (contain x, y), 3D (contain x, y, z), even 4D. 4D vectors can be used to describe something else, for example a color with an extra alpha value.
One of the toughest things beginners have difficulty with when it comes to vectors is to understand how something that seemingly looks like a point in space can be used to describe a direction.
Take the 2D vector (3,3). To understand how this represents a direction you need only look at the following graph. We all know that it takes two points to form a line. So what is the second point? The missing point is the origin located at (0,0). If we draw a line from the origin at (0,0) to (3,3) we get the following:
![Attached Image: vector.png]()
As you can see, the introduction of the origin as the second point gives our vector a direction. But you can also see that the first point (3,3) can be moved (or translated) closer to or farther away from the origin.
The distance from the origin is known as the magnitude and is given by the quadratic equation a^2 + b^2 = c^2. In this case 3^2 + 3^2 = c^2 and c = sqrt(18) ~= 4.24. If we divide each of the components of this vector by 4.24 we can scale the vector back to a point where it has a magnitude of just 1. We will learn in upcoming examples how this process of normalizing the vector can be very useful since this process retains the direction, but gives us an ability to scale the vector up or down quickly with simple multiplication by some numeric (aka scalar) value.
For the upcoming examples, I am going to assume that your math library uses Vector2 for a 2D vector and Vector3 for a 3D vector. There are various differences in naming across libaries and programming languages, for example vector, vector3, Vector3f, vec3, point, point3f and similar. Your math library must have some documentation and examples for them.
Like any other variable, the vector in your code has a meaning which is up to you: it can be a position, direction, velocity.
![Attached Image: file_pos.png]()
Vector addition is used to accumulate the difference described by both vectors into the final vector.
For example, if an object moves by A vector, and then by B vector, the result is the same as if it would have moved by C vector.
![Attached Image: file(4).png]()
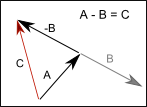
For subtraction, the second vector is simply inverted and added to the first one.
![Attached Image: file(5).png]()
If your vectors represent positions of objects A and B, then B - A will be a difference vector between positions. The result would represent a direction and a distance A must travel to get to B.
For example, to get a distance vector to that tree you need to subtract your position from the tree position.
![Attached Image: file(7).png]()
I am using pseudo-code to keep the code clean. Three numbers in parentheses (x, y, z) represent a vector.
Besides a position vector, object may have a velocity vector.
For example, the velocity vector for a cannon ball may describe the distance it is going to move over the next second.
When first fired, cannon ball may have these properties:
Every second, you would update cannon position based on the velocity:
Wait! We do not want to update object once per second. In fact, we want to do it as often as possible.
But we can not expect the time between updates to be fixed. So we use a delta time, which is the time since the last update.
Since our delta time represents a fraction of the time passed, we can use it to get only that fraction of our velocity for the next position update.
This is a very basic simulation. To make one, we model how our objects behave in our world (cannon ball has constant velocity forever). Then we load initial game state (cannon ball starts with initial velocity and position).
The final piece where everything comes together is an update loop, which is executed regularly We use the delta time (time interval) since the previous update, and update every simulated object to be where it should on the rules we defined (update cannon ball position based on its velocity).
Our cannon ball is quite boring: it will move to the same direction and at the same speed forever. We need it to react to the world around. For example, let there be gravity for it to fall, air resistance for it to slow down, and the wind just for kicks.
What the gravity actually means in a game? Well, it has a side effect of increasing velocity of objects to one direction: down. So in case our Y axis is up, our gravity vector would be:
So, before every update, we can modify our velocity:
Let's just say our air is thick. So thick it slows down cannon balls by half every second.
Velocity had the force because of the cannon ball being the cannon ball. Kinetic energy.
However, there might be another constant force to change the movement of cannon ball: like the wind.
The main point of this example is to demonstrate how easy it is to create quite complex behavior using a simple vector math.
Often you will not need a distance from A to B, just the direction for A to face the B. A distance vector B - A can represent the direction, but what if you need to move "just a bit" towards B, at the exact speed you like?
In such case vector length should be irrelevant If we reduce a direction vector to the length of 1, we can use it for this, and other purposes. We call this reduction the normalization and the resulting vector the normal vector.
![Attached Image: file(8).png]()
So, a normal vector always should be the length of 1, otherwise it is not a normal vector.
A normal vector represents an angle without any actual "angles" required as a possible change in position. If we multiply the vector by a scalar number, we get the direction vector that has the same length as the scalar.
There should be a "normalize" function in your math library to get a normal vector from any other vector.
So we can get a movement by exactly the 3 units towards B.
A normal vector can also be used to describe a direction a surface plane is facing. You can imagine the plane as an infinite slice of the world in half at a particular point P. Rotation of this slice is defined by the normal vector N.
![Attached Image: file(12)_no_j.png]()
To rotate this slice/plane, you would change its normal vector.
![Attached Image: g3841.png]()
A dot product is an operation on two vectors, which returns a number. You can think of this number as a way to compare the two vectors.
Usually written as:
This comparison is particularly useful between two normal vectors, because it represents a difference in rotation between them.
Here are the normal values in the illustration:
![Attached Image: file(10).png]()
Note that change from 1 to 0 and from 0 to -1 is not linear, but follows a cosine curve. So, to get an angle from a dot product, you need to calculate arc-cosine of it:
Suppose we are writing a light shader and we need to calculate the brightness of a pixel at a particular surface point. We have:
We can get the distance vector from our point to the light:
As well as the direction of the light for this particular point as a normal vector:
Then, using our knowledge about angle and dot product relationship, we can use dot product of point-to-light normal to calculate the brightness of the point. In simplest case it will be exactly equal the dot product!
![Attached Image: file(11).png]()
Believe it or not, this is the bare bones of a simple light shader. An actual fragment shader in OpenGL would look like this (do not worry if you have no knowledge of the shaders: this is just an example to demonstrate the practical application of dot product):
Note that the way "dot" and "normalize" functions are used is the only difference from previous examples.
To calculate the shortest distance from some point to a plane, first get distance vector to any point of that plane, do not normalize it, and multiply it with plane's normal vector.
If it's distance to a plane is 0, yes.
If this vector is perpendicular to plane's surface normal, then yes.
We already know that two vectors are perpendicular when their dot product is 0.
So vector is parallel to the plane when vector dot plane_normal == 0
Let's say our line starts at P1 and ends at P2. A point on plane surface SP and surface normal is SN.
If we make an imaginary plane run through the first line point P1, the solution boils down to calculating which point (P2 or SP) is both closer to P1 and more parallel to SN. This value for can be calculated by using a dot product.
![Attached Image: g3842.png]()
You can calculate "how much" it intersects the plane by comparing (dividing) these two values.
You can calculate the exact intersection point by multiplying line vector to u:
A cross product is also an operation on two vectors. The result is a third vector, which is perpendicular to the first two, and it's length is an average of the both lengths.
![Attached Image: file(13).png]()
Note that for cross product, the order of arguments matters. If you switch order, the result will be a vector of the same length, but facing the opposite direction.
Let's say an object moves into a wall at an angle. But wall is friction-less and object should slide along its surface instead of stopping. How to calculate its new position for that?
![Attached Image: file(14).png]()
First of all, we have a vector which represents the distance the object should have moved if there were no wall. We are going to call it a "change". Then, we are going to assume object is touching the wall. And we will also need the normal vector of this surface.
We will use the cross product to get a new vector which is perpendicular to the change and the normal:
Then, the final direction is perpendicular to this new vector and the same normal:
That's it:
With this article, I have tried to bridge the gap between the theory and the real practical application of it in game development. However, it means that I had to skip a lot of things in between.
But I hope the picture is a bit clearer. If anything, this walk-through may serve as a quick overview of the way Vector Math is used in Games.
Good news: use of trigonometry in graphics is rare and avoided for multitude of reasons. We have other tools which are easier to understand and use. You may recognize our old friend here - a vector.

This article will introduce you to 3D vectors and will walk you through several real-world usage examples. Even though it focuses on 3D, most things explained here also work for 2D.
Article assumes familiarity with algebra and geometry, some programming language, a basic knowledge of OOP.
Vector Math in Games
Concepts
In mathematics, a vector is a construct that represents both a direction as well as a magnitude. In game development it often can be used to describe a change in position, and can be added or subtracted to other vectors. You would usually find a vector object as part of some math or physics library.
They typically contain one or more components such as x, y and z. Vectors can be 1D (contain only x), 2D (contain x, y), 3D (contain x, y, z), even 4D. 4D vectors can be used to describe something else, for example a color with an extra alpha value.
One of the toughest things beginners have difficulty with when it comes to vectors is to understand how something that seemingly looks like a point in space can be used to describe a direction.
Take the 2D vector (3,3). To understand how this represents a direction you need only look at the following graph. We all know that it takes two points to form a line. So what is the second point? The missing point is the origin located at (0,0). If we draw a line from the origin at (0,0) to (3,3) we get the following:
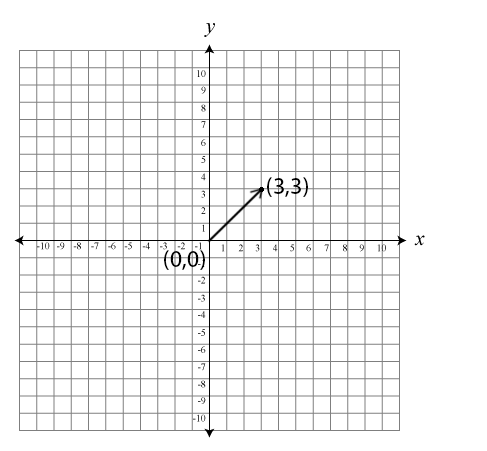
As you can see, the introduction of the origin as the second point gives our vector a direction. But you can also see that the first point (3,3) can be moved (or translated) closer to or farther away from the origin.
The distance from the origin is known as the magnitude and is given by the quadratic equation a^2 + b^2 = c^2. In this case 3^2 + 3^2 = c^2 and c = sqrt(18) ~= 4.24. If we divide each of the components of this vector by 4.24 we can scale the vector back to a point where it has a magnitude of just 1. We will learn in upcoming examples how this process of normalizing the vector can be very useful since this process retains the direction, but gives us an ability to scale the vector up or down quickly with simple multiplication by some numeric (aka scalar) value.
For the upcoming examples, I am going to assume that your math library uses Vector2 for a 2D vector and Vector3 for a 3D vector. There are various differences in naming across libaries and programming languages, for example vector, vector3, Vector3f, vec3, point, point3f and similar. Your math library must have some documentation and examples for them.
Like any other variable, the vector in your code has a meaning which is up to you: it can be a position, direction, velocity.
- Position - a vector represents an offset from your world origin point (0, 0, 0).
- Direction - vector looks very much like an arrow pointing at some direction. That is indeed what it can be used for. For example, if you have a vector that points south, you can make all your units go south.
- A special case of direction vector is a vector of length 1. It is called a normalized vector, or normal for short.
- A velocity vector can describe a movement. In that case, it is a difference in position over specific amount of time.
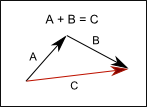
Remember the Basics - Vector Addition and Subtraction
Vector addition is used to accumulate the difference described by both vectors into the final vector.
For example, if an object moves by A vector, and then by B vector, the result is the same as if it would have moved by C vector.
For subtraction, the second vector is simply inverted and added to the first one.
Example: a Distance Between Objects
If your vectors represent positions of objects A and B, then B - A will be a difference vector between positions. The result would represent a direction and a distance A must travel to get to B.
For example, to get a distance vector to that tree you need to subtract your position from the tree position.
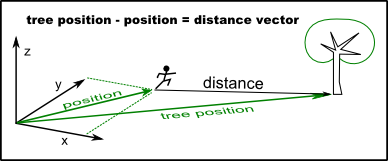
I am using pseudo-code to keep the code clean. Three numbers in parentheses (x, y, z) represent a vector.
tree_position = (10, 10, 0) my_position = (3, 3, 0) # distance and direction you would need to move # to get exactly where the tree is vector_to_tree = tree_position - my_position
Example: Velocity
Besides a position vector, object may have a velocity vector.
For example, the velocity vector for a cannon ball may describe the distance it is going to move over the next second.
When first fired, cannon ball may have these properties:
position = (0, 10, 10) # position: 10 units in Y and Z direction velocity = (500, 0, 0) # initial movement is 500 units in X direction over the next second
Every second, you would update cannon position based on the velocity:
position += velocity # add velocity to position and update position
Concept: Simulation
Wait! We do not want to update object once per second. In fact, we want to do it as often as possible.
But we can not expect the time between updates to be fixed. So we use a delta time, which is the time since the last update.
Since our delta time represents a fraction of the time passed, we can use it to get only that fraction of our velocity for the next position update.
position += velocity * delta
This is a very basic simulation. To make one, we model how our objects behave in our world (cannon ball has constant velocity forever). Then we load initial game state (cannon ball starts with initial velocity and position).
The final piece where everything comes together is an update loop, which is executed regularly We use the delta time (time interval) since the previous update, and update every simulated object to be where it should on the rules we defined (update cannon ball position based on its velocity).
Example: Gravity, Air Resistance and Wind
Our cannon ball is quite boring: it will move to the same direction and at the same speed forever. We need it to react to the world around. For example, let there be gravity for it to fall, air resistance for it to slow down, and the wind just for kicks.
What the gravity actually means in a game? Well, it has a side effect of increasing velocity of objects to one direction: down. So in case our Y axis is up, our gravity vector would be:
# increase velocity of every object -2 down per second gravity_vector = (0, -2, 0)
So, before every update, we can modify our velocity:
velocity += gravity_vector * delta # apply gravity effect position += velocity * delta # update position
Let's just say our air is thick. So thick it slows down cannon balls by half every second.
velocity += gravity_vector * delta # apply gravity effect velocity *= 0.5 * delta # apply 0.5 slowdown per second position += velocity * delta # update position
Velocity had the force because of the cannon ball being the cannon ball. Kinetic energy.
However, there might be another constant force to change the movement of cannon ball: like the wind.
# modify kinetic energy / velocity velocity += gravity_vector * delta # apply gravity effect velocity *= 0.5 * delta # apply 0.5 slowdown per second # add all forces final_change_per_second = velocity + wind_force_per_second # update position position += final_change_per_second * delta
The main point of this example is to demonstrate how easy it is to create quite complex behavior using a simple vector math.
Concept: Direction
Often you will not need a distance from A to B, just the direction for A to face the B. A distance vector B - A can represent the direction, but what if you need to move "just a bit" towards B, at the exact speed you like?
In such case vector length should be irrelevant If we reduce a direction vector to the length of 1, we can use it for this, and other purposes. We call this reduction the normalization and the resulting vector the normal vector.
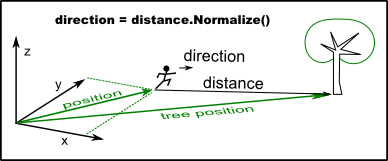
So, a normal vector always should be the length of 1, otherwise it is not a normal vector.
A normal vector represents an angle without any actual "angles" required as a possible change in position. If we multiply the vector by a scalar number, we get the direction vector that has the same length as the scalar.
There should be a "normalize" function in your math library to get a normal vector from any other vector.
So we can get a movement by exactly the 3 units towards B.
final_change = (B - A).normalize() * 3
Concept: Surface Plane
A normal vector can also be used to describe a direction a surface plane is facing. You can imagine the plane as an infinite slice of the world in half at a particular point P. Rotation of this slice is defined by the normal vector N.
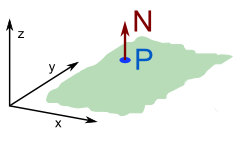
To rotate this slice/plane, you would change its normal vector.

Concept: Dot Product
A dot product is an operation on two vectors, which returns a number. You can think of this number as a way to compare the two vectors.
Usually written as:
result = A dot B
This comparison is particularly useful between two normal vectors, because it represents a difference in rotation between them.
- If dot product is 1, normals face the same direction.
- If dot product is 0, normals are perpendicular.
- If dot product is -1, normals face opposite directions.
Here are the normal values in the illustration:
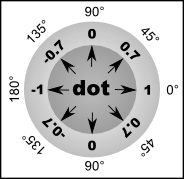
Note that change from 1 to 0 and from 0 to -1 is not linear, but follows a cosine curve. So, to get an angle from a dot product, you need to calculate arc-cosine of it:
angle = acos(A dot B)
Example: Light
Suppose we are writing a light shader and we need to calculate the brightness of a pixel at a particular surface point. We have:
- A normal vector which represent the direction of surface at this point.
- Position of the light.
- Position of this surface point.
We can get the distance vector from our point to the light:
distance_vec = light_pos - point_pos
As well as the direction of the light for this particular point as a normal vector:
light_direction = distance_vec.normalize()
Then, using our knowledge about angle and dot product relationship, we can use dot product of point-to-light normal to calculate the brightness of the point. In simplest case it will be exactly equal the dot product!
brightness = surface_normal dot light_direction
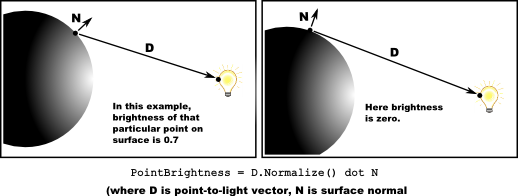
Believe it or not, this is the bare bones of a simple light shader. An actual fragment shader in OpenGL would look like this (do not worry if you have no knowledge of the shaders: this is just an example to demonstrate the practical application of dot product):
varying vec3 surface_normal;
varying vec3 vertex_to_light_vector;
void main(void)
{
vec4 diffuse_color = vec3(1.0, 1.0, 1.0); // the color of surface - white
float diffuse_term = dot(surface_normal, normalize(vertex_to_light_vector));
gl_FragColor = diffuse_color * diffuse_term;
}
Note that the way "dot" and "normalize" functions are used is the only difference from previous examples.
Example: Distance from a point to a plane
To calculate the shortest distance from some point to a plane, first get distance vector to any point of that plane, do not normalize it, and multiply it with plane's normal vector.
distance_to_a_plane = (point - plane_point) dot plane_normal;
Example: Is a point on a plane?
If it's distance to a plane is 0, yes.
Example: Is a vector parallel to a plane?
If this vector is perpendicular to plane's surface normal, then yes.
We already know that two vectors are perpendicular when their dot product is 0.
So vector is parallel to the plane when vector dot plane_normal == 0
Example: Line intersection with a plane
Let's say our line starts at P1 and ends at P2. A point on plane surface SP and surface normal is SN.
If we make an imaginary plane run through the first line point P1, the solution boils down to calculating which point (P2 or SP) is both closer to P1 and more parallel to SN. This value for can be calculated by using a dot product.

dot1 = SN dot (SP - P1) dot2 = SN dot (P2 - P1)
You can calculate "how much" it intersects the plane by comparing (dividing) these two values.
u = (SN dot (SP - P1)) / (SN dot (P2 - P1))
- if u == 0, line is parallel the plane.
- if u <= 1 and u > 0, line intersects the plane.
- if u > 1, no intersection.
You can calculate the exact intersection point by multiplying line vector to u:
intersection point = (P2 - P1) * u
Concept: Cross Product
A cross product is also an operation on two vectors. The result is a third vector, which is perpendicular to the first two, and it's length is an average of the both lengths.
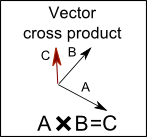
Note that for cross product, the order of arguments matters. If you switch order, the result will be a vector of the same length, but facing the opposite direction.
Example: Collision
Let's say an object moves into a wall at an angle. But wall is friction-less and object should slide along its surface instead of stopping. How to calculate its new position for that?
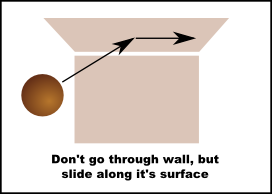
First of all, we have a vector which represents the distance the object should have moved if there were no wall. We are going to call it a "change". Then, we are going to assume object is touching the wall. And we will also need the normal vector of this surface.
We will use the cross product to get a new vector which is perpendicular to the change and the normal:
temp_vector = change cross plane_normal
Then, the final direction is perpendicular to this new vector and the same normal:
new_direction = temp_vector cross plane_normal
That's it:
new_direction = (change cross plane_normal) cross plane_normal
Now what?
With this article, I have tried to bridge the gap between the theory and the real practical application of it in game development. However, it means that I had to skip a lot of things in between.
But I hope the picture is a bit clearer. If anything, this walk-through may serve as a quick overview of the way Vector Math is used in Games.
More in-depth reading
- Vector Math - Addition, subtraction, negation, normalization.
- Better Explained Dot Product - Follows similar style of explaining dot product by examples
- Dot Product and Cross Product - More in-depth explanation of dot and cross products
- What is a game loop? - Short explanation of the game loop
- More in-depth look at the different update loop types